Dr Ma Guancong's Research Group - Experimental realization of unique non-Hermitian topological space

In our daily life, buildings are always erected uprightly, in which shops, offices, restaurants, etc. are placed in an orderly manner. In fact, these phenomena that we are familiar with are determined by geometry: on the scale of daily human life, space basically satisfies Euclidean geometry. More specifically, one of the salient features of Euclidean geometric space is that parallel lines never intersect. As we all know, the three-dimensional Euclidean space can be completely characterized by a three-dimensional coordinate system consists of three mutually perpendicular coordinate axes known as x, y, and z. However, not all objects can be embedded in Euclidean space. For example, the Penrose stairs seen in science fiction movies cannot be constructed in three-dimensional space. It turns out that there actually exist many types of geometric spaces. Take the earth for example, the earth itself is a sphere, but the geometry of this sphere does not satisfy Euclidean geometry. For instance, any two parallel meridians can intersect at the north or south poles, and the sum of internal angles of a triangle that is randomly cut from this sphere is not equal to 180 degrees. From these examples, it is apparent that the properties of geometric space also have a critical impact on the laws of physics.

As the abstraction of geometry, topology is also a branch of mathematics. (For example, the English letter "B" can be transformed into the Arabic numeral "8" by stretching, while the English letter "D" fails to be changed into "8" by stretching, due to the fact that the topological properties of "8" are similar to "B" but different from "D".) In that sense, topology is of extremely profound importance to physics. Moreover, the 2016 Nobel Prize in Physics was awarded to three scientists for their outstanding contributions to the application of topology in physics. In this study, we realized a geometric space called Riemannian manifold by introducing two complex parameters into an acoustic system, and then characterized its special topological properties both theoretically and experimentally. Particularly, the system can produce a unique singularity in a specific parameter space, which is also referred to as a higher-order exceptional point. The Riemannian manifold of higher-order exceptional point will bifurcate into multiple intersecting surfaces. As a consequence, the evolution process of the system around an exceptional point can reflect the geometric characteristics of these Riemann surfaces as well as the unique topological properties of the exceptional point. When the system evolves around an exceptional point, the eigenmodes of the system will exchange, resulting in fractional topological charges. More interestingly, there is a continuous curve composed of low-order singularities near the high-order singularities. Therefore the parameter space is cut as cracked glass and is no longer continuous, which results in different windings of the higher-order exceptional point, so that we can simultaneously get different topological charges for the same exceptional point. Through the actual measurement in the experiment, the experimental results are completely consistent with the theoretical results.

This project demonstrates both theoretically and experimentally a unique order-3 exceptional point with two different topological charges, which is of great significance in the research field of the topological properties of non-Hermitian systems. Additionally, this study not only paves a new way for the related researches and applications of non-Hermitian systems and their topological properties, but also provides new directions for the applications of optics and acoustics.

The research result is titled Exceptional Nexus with A Hybrid Topological Invariant and published online in the journal Science. [Science 370, 1077-1080 (2020).]
 

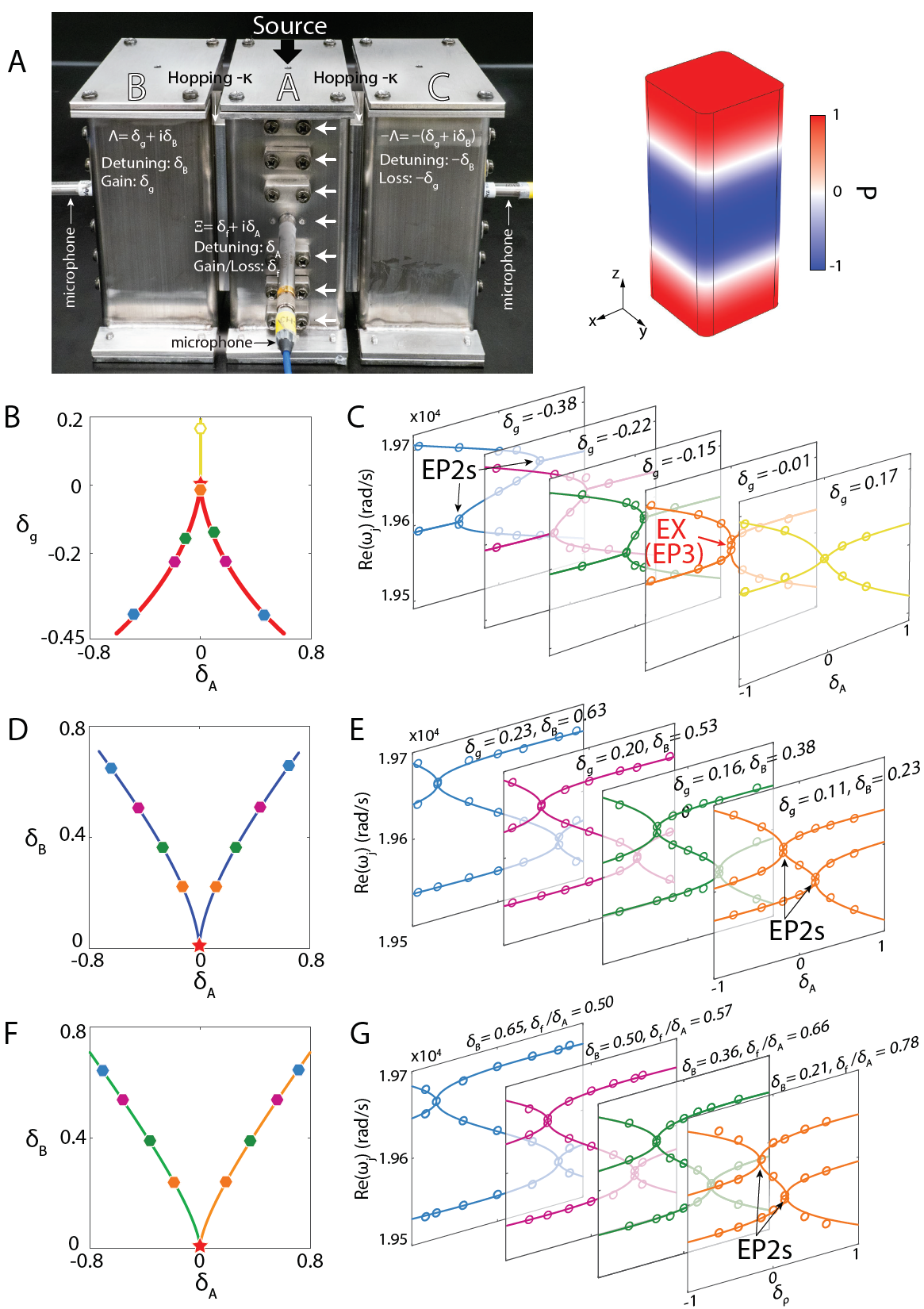
Figure 1. Acoustic experimental setup

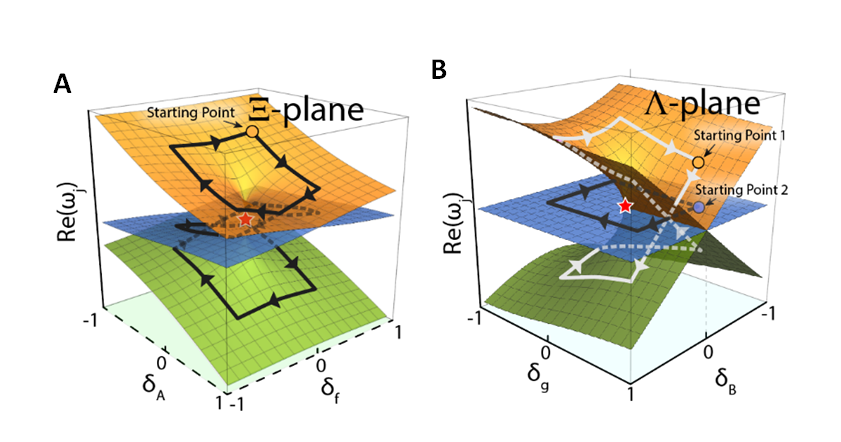
Figure 2. Riemannian manifold of the system

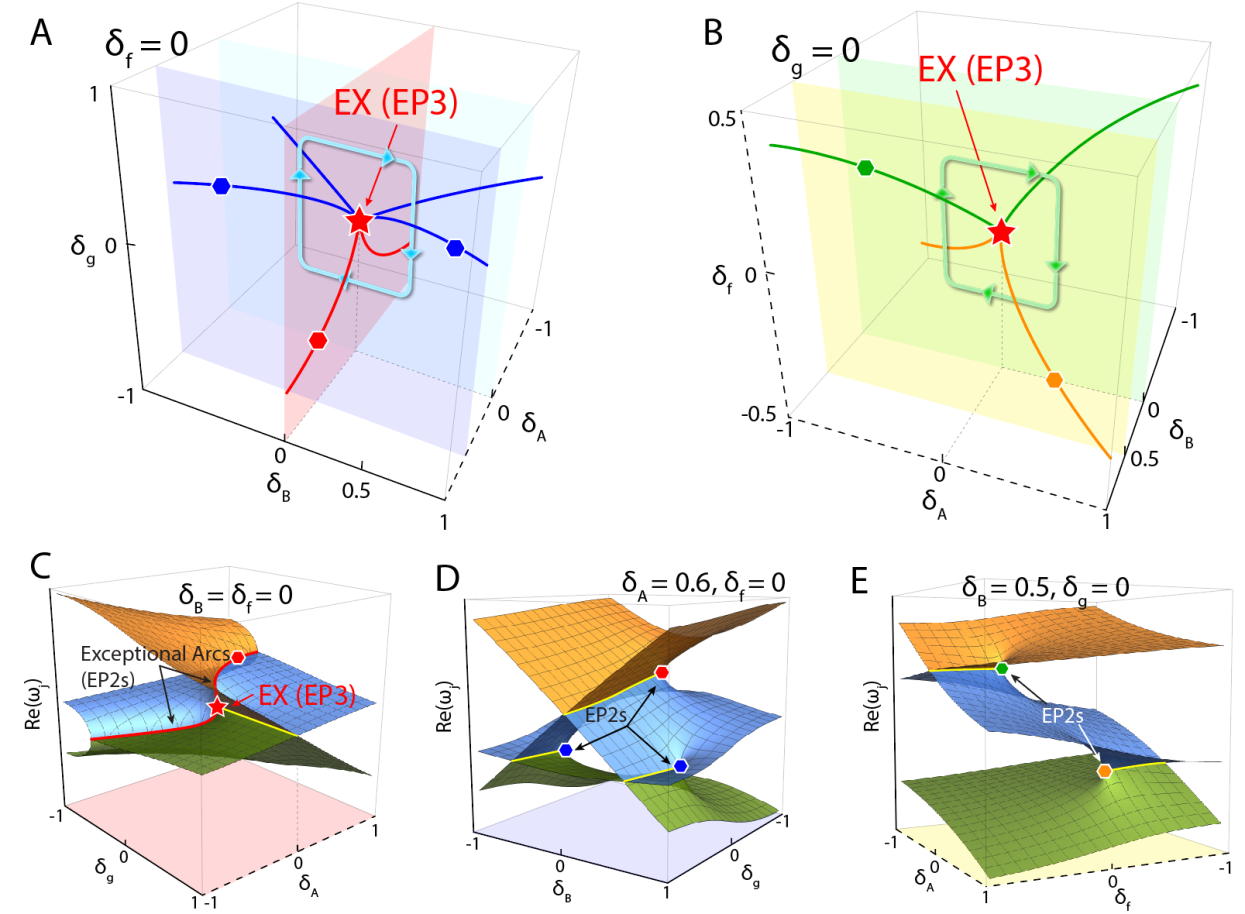
Figure 3. Multiple exceptional arcs are connected to form an exceptional nexus under certain parameters

实现特殊的非厄米拓扑空间

日常生活中，楼房总是笔直竖立，而家居、办公室、餐厅等总是水平有序地被安放其中。这些我们习以为常的现象，归根结底是由几何决定的：在人类日常生活这个尺度上，空间基本满足欧几里得几何。欧氏几何空间的显著特征之一，就是平行线永不相交。而三维欧氏空间可以通过我们所熟知的x,y,z三个相互垂直的坐标系来完整表征。然而，并非所有形状都能嵌入在欧氏空间中，例如科幻电影中常见的彭罗斯阶梯，就无法在三维空间中被建造出来。这也从一个测面说明，几何空间实际上有着繁多的种类。拿我们所居住的地球来说，地球本身是个球面，而球面上几何就不满足欧氏几何。比如，任何两条平行的经线却可以在南北极相交，而从球面随便切一块三角形，其内角和也不是180度。从上面的例子延伸，不难想象，几何空间的性质对物理定律也有着十分深刻的影响。

拓扑学正是对几何的抽象化的一个数学分支。（举个例子，英文字母“B”可以通过拉伸转化为阿拉伯数字“8”，而英文字母“D”却不能靠拉伸转化为阿拉伯数字“8”，因为“8”和“B”的拓扑特性相同，而与“D”不同。）因此，拓扑对物理有着非凡的深刻意义。2016年的诺贝尔物理学奖正是颁给了三位对拓扑在物理学中的应用做出开创性贡献的科学家。我们在该研究中，通过在声学系统引入复参数，实现了一种叫做黎曼流形的几何空间，并从理论和实验表征了其特殊的拓扑性质。值得注意的是，系统在参数空间中能产生一种特有的奇点——高阶奇异点(higher-order exceptional point)。高阶奇异点的黎曼流形会出现分岔成多个相互交叉的面。系统在绕奇异点的演化过程就能体现其这些黎曼面的几何特性，体现独特的拓扑性质。当系统围绕着奇异点演化时，本征模会发生交换，从而产生分数拓扑荷。更有意思的是，高阶奇异点附近存在着低阶奇异点构成的连续曲线。参数空间因此被切割，正好比开裂的玻璃不再连续。该特性造就了高阶奇异点不同的卷绕，因此我们能对同一个点同时得到不同的拓扑荷。通过实验的实际测量，得到的实验结果与理论结果完全吻合。

本课题在理论上和实验上同时展示具有两种不同的拓扑荷的特殊三阶奇异点，这在非厄米系统的拓扑特性研究领域中，意义非凡。这为非厄米系统及其拓扑特性的相关研究和应用开辟新的方向，并对光学、声学等应用提供了新的方向。

该成果以Exceptional Nexus with A Hybrid Topological Invariant为题，在线发表在《科学》（Science）期刊上。[Science 370, 1077-1080 (2020).]

图1 声学实验装置

图2  系统的黎曼流形
 

图3 特定参数下多条奇异弧联结形成奇异联结点