New Symmetry Unlocks a Chain of Exceptional Points in Non-Hermitian Mechanical Systems

A recent study co-organised by  Professor Guancong MA from the Department of Physics at HKBU and Dr Xiaohan CUI from the Department of Physics at HKUST have found a new type of topological structure called "exceptional chains" that is protected by a hidden symmetry in mechanical systems. In recent years, researchers have been studying exceptional points (EPs), which are unique features found in non-Hermitian systems that don't follow the usual rules of energy conservation. Previous studies on EPs focused on equations that depict specific systems, such as quantum mechanics, where the time derivative is of the first order. However, this new research shows that mechanical systems, described by second-order differential equations, also have hidden symmetries and novel properties related to EPs, which have been largely overlooked until now.

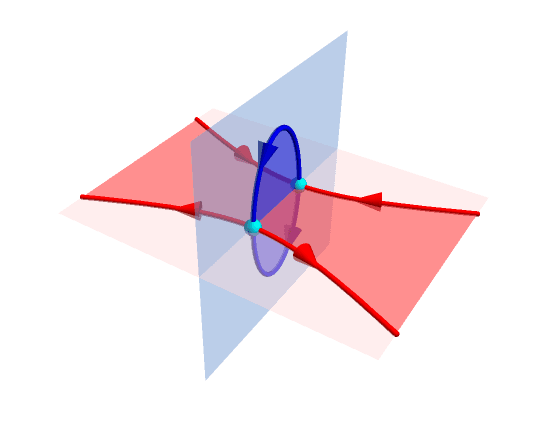
Fig.1 The directed exceptional lines (red and blue line) stably connect in a chain-like manner.

Fig. 2 Photo of the experimental setup

The researchers discovered a specific type of symmetry unique to mechanical systems, which they called non-Hermitian latent symmetries. These symmetries play a crucial role in enabling continuous curves formed by EPs to stably connect in a chain-like manner (see Fig. 1). The scientists were able to confirm this discovery by building a mechanical system composed of springs and programmable motors (see Fig. 2). This research opens up new possibilities in the field of non-Hermitian topology and encourages further exploration of classical systems governed by second-order differential equations. These findings have implications for various fields, including mechanics, electricity, optomechanics, and micro-electromechanical systems.

The journal titled “Experimental Realization of Stable Exceptional Chains Protected by Non-Hermitian Latent Symmetries Unique to Mechanical Systems” was published in Physical Review Letters. 

Click here to learn more about Professor Ma.